Alternativa didáctica para un aprendizaje contextualizado de la disciplina análisis matemático
Palabras clave:
aprendizaje contextualizado, Análisis Matemático, accionesResumen
El proceso de enseñanza-aprendizaje de la disciplina Análisis Matemático solo se puede entender si su estudio se hace desde la integración de referentes filosóficos, sociológicos, psicológicos, pedagógicos y didácticos. Este proceso se enmarca en las tendencias actuales que persiguen la participación activa y consciente de los estudiantes en un proceso de aprendizaje desarrollador, pero existen insuficiencias en el aprendizaje de los contenidos de esta disciplina por los estudiantes de la carrera Matemática de la Universidad de Las Tunas. El trabajo que se presenta es un resultado de la línea de investigación Influencia del contexto en la didáctica de las Ciencias Exactas en el siglo XXI. En él se ofrece una alternativa para un aprendizaje contextualizado de los contenidos de la disciplina Análisis Matemático de la carrera Matemática, debido a que las insuficiencias que se manifiestan en el proceso de enseñanza aprendizaje de esta disciplina afectan la eficiencia de la carrera. Esto se hizo tomando los niveles de desarrollo de los involucrados como fundamento desde el Enfoque Histórico-Cultural. La esencia consistió en la utilización de acciones a realizar por los estudiantes y los docentes que permitan desarrollar un proceso de enseñanza-aprendizaje desarrollador, con un diagnóstico pedagógico integral como trasfondo. Durante su desarrollo se utilizaron diversos métodos de nivel teórico y empírico.
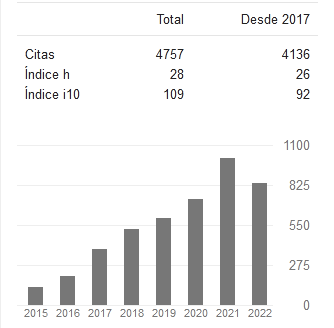
Citas
Báez, N. (2018). Estrategia didáctica para la formación de conceptos en el proceso de enseñanza-aprendizaje del Cálculo Diferencial de una variable real en las carreras de ingeniería. [Tesis doctoral], Universidad de Camagüey
Castellanos, D., Castellanos, B., Llivina, M. J., Silverio, M., Reinoso, C. y García, C. (2002). Aprender y enseñar en la escuela: una concepción desarrolladora. Pueblo y Educación.
Cuevas, A., Martínez, M. y Pluvinage, F. (2012). Promoviendo el pensamiento funcional en la enseñanza del cálculo: un experimento con el uso de tecnologías digítales y sus resultados. Annales de Didactique et de Sciences Cognitivaes, (17), 137-168.
Katz, K. & Katz, M. (2010). Zooming in On Infinitesimal in a Post-Triumvirate Era. Educational Studies in Mathematics, 74(3), 259-273.
MES. (2016). Modelo del Profesional. Plan de Estudio “E”. Carrera: Licenciatura en Educación. Matemática. [Material digital]
Ochoa, E. L. (2014). Procedimiento didáctico para favorecer el aprendizaje de las funciones reales de una variable real en el proceso de enseñanza-aprendizaje de la disciplina Análisis Matemático. [Tesis de Maestría], UCP “Pepito Tey”.
Van de Sade, C. (2011). A description and Characterization of Student Activity in an Open, Online, Mathematics Help Forum. Educational Studies in Mathematics, 77(1), 53-78.
Publicado
Cómo citar
Número
Sección
ARK
Licencia
Derechos de autor 2023 Enma Leticia Ochoa Domínguez , Nohemí Rodríguez Morffi , Yohania Yoppiz Fuentes

Esta obra está bajo una licencia internacional Creative Commons Atribución 4.0.
Usted es libre de:
- Compartir — copiar y redistribuir el material en cualquier medio o formato
- Adaptar — remezclar, transformar y construir a partir del material para cualquier propósito, incluso comercialmente.
Bajo los siguientes términos:
- Atribución — Usted debe dar crédito de manera adecuada, brindar un enlace a la licencia, e indicar si se han realizado cambios. Puede hacerlo en cualquier forma razonable, pero no de forma tal que sugiera que usted o su uso tienen el apoyo de la licenciante.
- No hay restricciones adicionales — No puede aplicar términos legales ni medidas tecnológicas que restrinjan legalmente a otras a hacer cualquier uso permitido por la licencia.