La inversión, teoría y recomendaciones metodológicas para su tratamiento
Palabras clave:
inversión matemática, planteo y resolución de problemas, recomendaciones metodológicasResumen
En la investigación se expone de manera lógica y deductiva la teoría de inversión. Para ello, se exponen las principales definiciones y teoremas que caracterizan a la transformación, se incluyen teoremas que constituyen recursos complementarios de valor para la solución de problemas de geometría plana en las modalidades de cálculo. Además, se incluyen demostraciones y construcciones auxiliares, así como recomendaciones metodológicas para el tratamiento de este contenido con el objetivo de lograr mayor desarrollo y flexibilidad en el pensamiento dentro del proceso de enseñanza-aprendizaje de la Matemática. Estas recomendaciones metodológicas están dirigidas a lograr que los estudiantes construyan la mayor parte del conocimiento, los cuales se utilizarán posteriormente en el planteo y la resolución de problemas.
Descargas
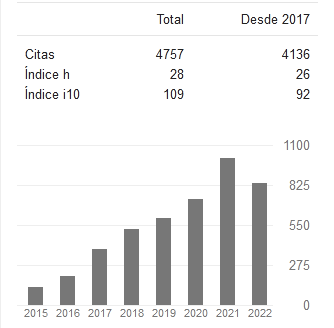
Citas
Aldazabal Melgar, Omar Franco, Vértiz Osores, Ricardo Iván, Zorrilla Tarazona, Eduardo, Aldazábal Melgar, Liliana Hilda, & Guevara Duarez, Manuel Felipe. (2021). Software GeoGebra en la mejora de capacidades resolutivas de problemas de figuras geométricas bidimensionales en universitarios. Propósitos y Representaciones, 9(1). https://dx.doi.org/10.20511/pyr2021.v9n1.1040
Badillo-Torres, V., & Rodríguez-Abitia, G. (2021). Plataforma Virtual para el aprendizaje de la Geometría Analítica. Revista Internacional De Pedagogía E Innovación Educativa, 2(1), pp. 123–138. https://doi.org/10.51660/ripie.v2i1.94
Carmenates Barrios, Osmany Alfredo, & Tarrío Mesa, Kirya. (2019). El pensamiento lógico, psicológico y social: su contribución a la resolución de problemas geométricos. Conrado, 15(69), pp. 362-369. http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S1990-86442019000400362&lng=es&tlng=es.
Figueroa, L. G. (2017). Una transformación inspirada en la inversión respecto a la elipse. http://hdl.handle.net/20.500.12209/9761.
González, Fernando (2020). La matemática y el arte en el proceso de enseñanza aprendizaje de la geometría. En Balda, Paola; Parra, Mónica Marcela; Sostenes, Horacio (Eds.), Acta Latinoamericana de Matemática Educativa, pp. 368-379. México, DF: Comité Latinoamericano de Matemática Educativa.
Lugo de Acosta, C. A. (2021). Efectos de la aplicación del software GeoGebra para la enseñanza – aprendizaje semi-presencial de la Geometría Analítica en el nivel universitario. INNOVA UNTREF, 1(3). http://revistas.untref.edu.ar/index.php/innova/article/view/979
Molina, A. B., Arenas Díaz, J. E., & Pineda Ballesteros, E. (2019). El aprendizaje de la geometría con Geogebra, un enfoque de aprendizaje por problemas. Revista Docencia Universitaria, 20(2), pp. 55–67. https://revistas.uis.edu.co/index.php/revistadocencia/article/view/10522
Oliver, M.; Valdez, G.; Vecino, S.; Astiz, M. (2018). Complementando la formación geométrica de los futuros profesores. En Lestón, Patricia (Ed.), Actas de la XII Conferencia argentina de educación matemática, pp. 1-8. http://funes.uniandes.edu.co/19553/
Roanes Lozano, Eugenio (1993). Automatización e implementación de algunos problemas algebráicos y geométricos. Tesis (Doctoral), Facultad de Informática (UPM). https://doi.org/10.20868/UPM.thesis.10113.
Rojas, R. (2020). Introducción del GeoGebra en el proceso de enseñanza–aprendizaje de Geometría a docentes en formación. Revista Caribeña de Investigación Educativa, 4(1). http://52.225.194.101/index.php/recie/article/view/174
Urrego Gómez, Y. (2021). Propuesta metodológica para la enseñanza-aprendizaje de la geometría mediada por los conceptos de área y volumen a partir del estudio de los polígonos regulares en el gado sexto de la I. E. Dinamarca. Universidad Nacional de Colombia.
Publicado
Cómo citar
Número
Sección
ARK
Licencia
Derechos de autor 2023 Diógenes Feliciano González Hernández, Miguel Eduardo González Díaz, Nolbert González Hernández

Esta obra está bajo una licencia internacional Creative Commons Atribución 4.0.
Usted es libre de:
- Compartir — copiar y redistribuir el material en cualquier medio o formato
- Adaptar — remezclar, transformar y construir a partir del material para cualquier propósito, incluso comercialmente.
Bajo los siguientes términos:
- Atribución — Usted debe dar crédito de manera adecuada, brindar un enlace a la licencia, e indicar si se han realizado cambios. Puede hacerlo en cualquier forma razonable, pero no de forma tal que sugiera que usted o su uso tienen el apoyo de la licenciante.
- No hay restricciones adicionales — No puede aplicar términos legales ni medidas tecnológicas que restrinjan legalmente a otras a hacer cualquier uso permitido por la licencia.