IMPLEMENTACIÓN DEL IDIOMA INGLÉS Y OTRAS ESTRATEGIAS CURRICULARES PARA FORMACIÓN INTEGRAL. EJEMPLOS DESDE PROBABILIDADES Y ESTADÍSTICAS
Palabras clave:
Estrategias curriculares; inglés; Probabilidades; Estadísticas.Resumen
Las estrategias curriculares incorporan un nuevo aspecto a la visión de las características del proceso de formación. Este concepto expresa una cualidad igualmente necesaria al concebir el plan de estudio de una carrera universitaria, y está relacionado con aquellos objetivos generales que no es posible alcanzar, con el nivel de profundidad y dominio requeridos, desde el contenido de una sola disciplina y demandan el concurso adicional de las restantes. Sin embargo, es insuficiente la concreción que logran los docentes de las estrategias curriculares en el proceso de enseñanza aprendizaje y la preparación que realizan de las asignaturas que imparten presenta limitaciones en el diseño y tratamiento a estas. Esto se revierte en que los estudiantes presentan carencias en el empleo de los recursos informáticos a su disposición, en la comunicación en idioma inglés, su formación económica, la dimensión ambiental y en el manejo adecuado de la información científico y técnica, limitaciones que deben ser atendidas desde un sistema coherente de influencias que permita contribuir a su formación integral. Así es que el objetivo de este artículo es orientar a los docentes hacia la implementación de las estrategias curriculares para el desarrollar procesos de enseñanza-aprendizaje en la carrera, a partir de la demostración de formas en que se puede desarrollar teniendo en cuenta el aprovechamiento de las potencialidades del contenido en las clases de las asignaturas que imparten. Esto se hace tomando como ejemplos los contenidos de la disciplina Probabilidades y Estadísticas, de la Licenciatura en Educación, con especialidad en Matemática-Física.
Descargas
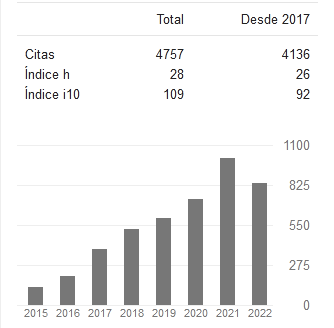
Citas
Amat, M., González, O., Gamboa, M.E. y Carmenates, O.A. (2009). Problemas de razonamiento lógico. Revista Opuntia Brava, 1(3).
Cantón, J. (2011). Ejercicios y problemas integradores de Matemática para los estudiantes de Secundaria Básica. La Habana: Editorial Pueblo y Educación.
Colectivo de autores. (2012). Modelo del Profesional carrera de Licenciatura en Educación, especialidad Matemática–Física (Plan de Estudio “D”). La Habana.
Fernández, H. y Gamboa, M.E. (2005). Actividades en las que se pone de manifiesto el uso de los medios de enseñanza en forma de sistema para la enseñanza de la Geometría. Boletín de la Sociedad Cubana de Matemática y Computación, 3(1).
Freund, J. E. (1987). Estadística elemental moderna. Ed: Revolucionaria.
Gamboa, M.E. (2006). Aprendizaje y enseñanza de la matemática tomando como bases sus aplicaciones prácticas. In VI Congreso Internacional Virtual de Educación.
Gamboa, M.E. (2007). El diseño de unidades didácticas contextualizadas para la enseñanza de la Matemática en la Educación Secundaria Básica. Tesis en opción al Grado Científico de Doctor en Ciencias Pedagógicas. Las Tunas.
Gamboa, M.E. (2012a). Enfoque vigotskiano del curriculum en la Pedagogía contemporánea. Unidades didácticas contextualizadas. Saarbrucken, Alemania: Editorial Académica Española.
Gamboa, M.E. (2012b). Unidades didácticas contextualizadas para enseñar matemáticas. Saarbrucken, Alemania: Editorial Académica Española.
Gamboa, M.E. (2013a). Situación actual de la Disciplina Principal Integradora Formación Laboral-Investigativa en la carrera Matemática-Física. Recuperado de http://roa.ult.edu.cu/jspui/handle/123456789/3950
Gamboa, M.E. (2013b). Regla de Gamboa para la división entera de polinomios y triángulos de Michel para la Geometría fractal. Opuntia Brava, 5(3).
Gamboa, M. E., Carmenates, O. A., Borrego, A. y Fernández, H. (2005). Pizarra, papel, computadora: un sistema de medios para la enseñanza de la Geometría. In V Congreso Internacional Virtual de Educación.
Gamboa, M.E., Carmenates, O.A. y Amat, M. (2010). El legado de Vigotsky en la profesión educativa. Opuntia Brava, 2(2).
Gamboa, M.E. y Carmenates, O.A. (2011). Influencia del pensamiento vigotskiano en el nivel micro del diseño curricular. Opuntia Brava, 3(1).
Gamboa, M.E. y Cortina, V.M. (2012). Modelo para el diseño de unidades didácticas contextualizadas. Opuntia Brava, 4(4).
Gamboa, M.E. y Santiesteban, D. (2013). Regla de Gamboa y divenpo: novedoso procedimiento y software para la división entera de polinomios. En B. Almeida (Presidencia), Estrategias para la enseñanza de la Matemática, la Estadística y la Computación. Simposio llevado a cabo en el XV Evento Internacional La enseñanza de la Matemática, la Estadística y la Computación Matecompu 2013, Matanzas, Cuba.
Horruitiner, P. (2006). El proceso de formación en la universidad cubana. Pedagogía Universitaria, 11(3), 1-15.
Horruitiner, P. (2009). La universidad cubana: modelo de formación. Editorial Universitaria del Ministerio de Educación Superior. Ciudad de La Habana.
MES (2003). Documento base para la elaboración de los planes de estudio "D". La Habana: MES.
Mode, E. (1966). Elements of Probability and Statistics. Prentice-Hall, international, Inc.
Rodríguez, M., Gamboa, M.E. y García, M. (2013). La autoevaluación de la carrera en función de elevar la calidad en la formación del profesional de la Educación. En M. Toro (Presidencia), Taller de Educación Superior y sus Perspectivas. Simposio llevado a cabo en el Evento provincial del Congreso Internacional de Universidad 2014, Las Tunas, Cuba.
Ruiz, L. (2007). Formación integral: desarrollo intelectual, emocional, social y ético de los estudiantes. Revista universitaria de sonora,(1), 11-13.
Spiegel, M. R. (1961). Theory and problems of Statistics. Schaum’s Outline Series. McGraw-Hill Book Company.
Spiegel, M. R. (1986). Teoría y problemas de Estadística. Ed: Revolucionaria.
Descargas
Publicado
Cómo citar
Número
Sección
Licencia
Derechos de autor 2020 Michel Enrique Gamboa Graus, René Yasmani Velázquez Prieto

Esta obra está bajo una licencia internacional Creative Commons Atribución 4.0.
Usted es libre de:
- Compartir — copiar y redistribuir el material en cualquier medio o formato
- Adaptar — remezclar, transformar y construir a partir del material para cualquier propósito, incluso comercialmente.
Bajo los siguientes términos:
- Atribución — Usted debe dar crédito de manera adecuada, brindar un enlace a la licencia, e indicar si se han realizado cambios. Puede hacerlo en cualquier forma razonable, pero no de forma tal que sugiera que usted o su uso tienen el apoyo de la licenciante.
- No hay restricciones adicionales — No puede aplicar términos legales ni medidas tecnológicas que restrinjan legalmente a otras a hacer cualquier uso permitido por la licencia.